Heron’s Formula: NCERT Maths Class 9

Have you ever needed to find the area of a triangle but didn’t know its height? Don’t worry! Heron’s Formula is here to help. This formula allows you to calculate the area of a triangle using only the lengths of its three sides—no height required!

What is Heron’s Formula?

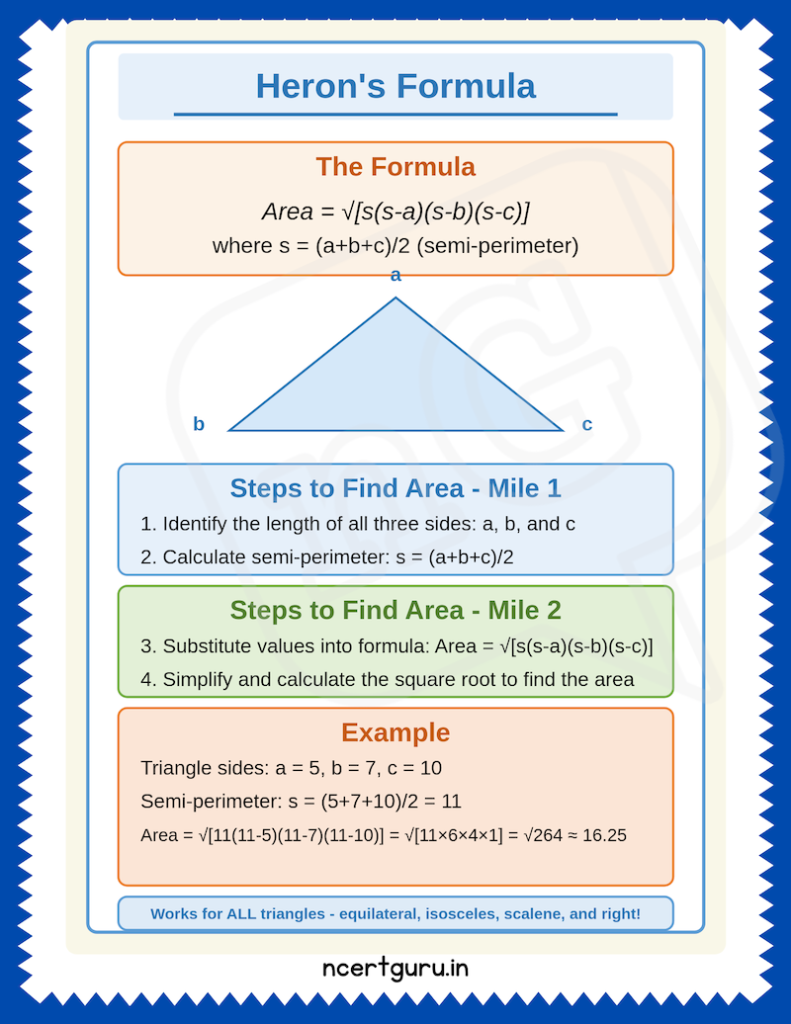
Heron’s Formula lets you find the area of any triangle when you know the length of its three sides. No need for angles, heights, or other measurements.

The formula looks like this:

Area = √[s(s-a)(s-b)(s-c)]

Where:

• a, b, and c are the three sides of the triangle
• s is the semi-perimeter (half the perimeter): s = (a+b+c)/2

Does Heron’s Formula Work For All Triangles?

Yes! That’s the beauty of this Formula. It works for:

• Right triangles
• Equilateral triangles (all sides equal)
• Isosceles triangles (two sides equal)
• Scalene triangles (all sides different)

No matter what shape your triangle is, as long as you know the three sides, you can find its area.

Why Do We Need It?

Normally, to find a triangle’s area, we use: Area = ½ × base × height

But what if we don’t know the height? Measuring it might be hard or impossible in real-world problems. Heron’s Formula saves the day!

Let’s Try An Example

Let’s try an example:

Problem: Find the area of a triangle with sides 5 cm, 6 cm, and 7 cm.

Step 1: Calculate the Semi-Perimeter (s)

s=5+6+72=182=9 cms=25+6+7​=218​=9 cm

Step 2: Plug Values into Heron’s Formula

Area=9(9−5)(9−6)(9−7)Area=9(9−5)(9−6)(9−7)​=9×4×3×2=9×4×3×2​=216≈14.7 cm2=216​≈14.7 cm2

Answer: The area is about 14.7 cm².

Where Did This Formula Come From?

Heron (or Hero) of Alexandria, who lived around 10-70 CE in Egypt, discovered this formula. He was a great mathematician who wrote about many practical math applications.

Why Heron’s Formula Matters Today

We still use this formula for:

• Land surveying
• Construction projects
• Computer graphics
• Navigation systems

Next time you face a triangle and know its three sides, you won’t have to worry about heights or angles.Just reach for Heron’s Formula and solve it!

Remember:
✅ Find the semi-perimeter (s) first.
✅ Plug the values into the formula.
✅ Works for all types of triangles!

From Mathematics Textbook, NCERT Maths Class 9

NCERT Solutions for Class 9 Maths to EXERCISE 10.1

Question 1: A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?

Solution

For an equilateral triangle, all sides are equal to ‘a’.

Step 1: Find the semi-perimeter s. s = (a + a + a)/2 = 3a/2

Step 2: Apply Heron’s formula. Area = √[s(s-a)(s-a)(s-a)] = √[(3a/2)(3a/2-a)(3a/2-a)(3a/2-a)] = √[(3a/2)(a/2)(a/2)(a/2)] = √[(3a/2)(a/2)³] = √[3a⁴/16] = (√3/4)a²

Now, if the perimeter is 180 cm, then: 3a = 180 cm a = 60 cm

Area = (√3/4)(60)² = (√3/4)(3600) = 900√3 cm² ≈ 1559.37 cm²

Question 2:The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m. The advertisements yield an earning of ₹5000 per m² per year. A company hired one of its walls for 3 months. How much rent did it pay?

Solution

Given: a = 122 m, b = 22 m, c = 120 m Rate = ₹5000 per m² per year Period = 3 months = 3/12 = 1/4 year

Step 1: Find the semi-perimeter s. s = (122 + 22 + 120)/2 = 264/2 = 132 m

Step 2: Apply Heron’s formula. Area = √[s(s-a)(s-b)(s-c)] = √[132(132-122)(132-22)(132-120)] = √[132 × 10 × 110 × 12] = √[17,424,000] = 4,174.2 m²

Step 3: Calculate the rent. Rent = Area × Rate × Time period = 4,174.2 × 5000 × (1/4) = ₹5,217,750

Therefore, the company paid ₹5,217,750 as rent for 3 months.

Question 3: There is a slide in a park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN”. If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.

Solution

Given: a = 15 m, b = 11 m, c = 6 m

Step 1: Find the semi-perimeter s. s = (15 + 11 + 6)/2 = 32/2 = 16 m

Step 2: Apply Heron’s formula. Area = √[s(s-a)(s-b)(s-c)] = √[16(16-15)(16-11)(16-6)] = √[16 × 1 × 5 × 10] = √[800] = 28.28 m²

Therefore, the area painted in colour is 28.28 m².

Question 4: Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.

Solution

Given: a = 18 cm, b = 10 cm, perimeter = 42 cm

Step 1: Find the third side c. Perimeter = a + b + c 42 = 18 + 10 + c c = 42 – 28 = 14 cm

Step 2: Find the semi-perimeter s. s = (18 + 10 + 14)/2 = 42/2 = 21 cm

Step 3: Apply Heron’s formula. Area = √[s(s-a)(s-b)(s-c)] = √[21(21-18)(21-10)(21-14)] = √[21 × 3 × 11 × 7] = √[4,851] = 69.65 cm²

Therefore, the area of the triangle is 69.65 cm².

Question 5: Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm. Find its area.

Solution

Given: Ratio of sides = 12 : 17 : 25 Perimeter = 540 cm

Step 1: Find the actual sides. Let the sides be 12x, 17x, and 25x. Perimeter = 12x + 17x + 25x = 540 54x = 540 x = 10

So, a = 12 × 10 = 120 cm b = 17 × 10 = 170 cm c = 25 × 10 = 250 cm

Step 2: Find the semi-perimeter s. s = (120 + 170 + 250)/2 = 540/2 = 270 cm

Step 3: Apply Heron’s formula. Area = √[s(s-a)(s-b)(s-c)] = √[270(270-120)(270-170)(270-250)] = √[270 × 150 × 100 × 20] = √[81,000,000] = 9,000 cm²

Therefore, the area of the triangle is 9,000 cm².

Question 6: An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.

Solution

Given: Perimeter = 30 cm Two equal sides = 12 cm each

Step 1: Find the third side. Perimeter = a + b + c 30 = 12 + 12 + c c = 30 – 24 = 6 cm

Step 2: Find the semi-perimeter s. s = (12 + 12 + 6)/2 = 30/2 = 15 cm

Step 3: Apply Heron’s formula. Area = √[s(s-a)(s-b)(s-c)] = √[15(15-12)(15-12)(15-6)] = √[15 × 3 × 3 × 9] = √[1,215] = 34.86 cm²

Therefore, the area of the isosceles triangle is 34.86 cm².