The volume of a cone is a very important concept in geometry. It tells us how much space is inside a cone-shaped object, like an ice cream cone or a party hat. You’ll learn how to use the formula and solve questions.
📌What is a Cone?
A cone is a 3D shape. It has:
- A flat circular base,
- A pointed top (called the vertex),
- And a curved surface.
Imagine a birthday cap or an ice cream cone — that’s the shape of a cone.
📌 Volume of a Cone Formula
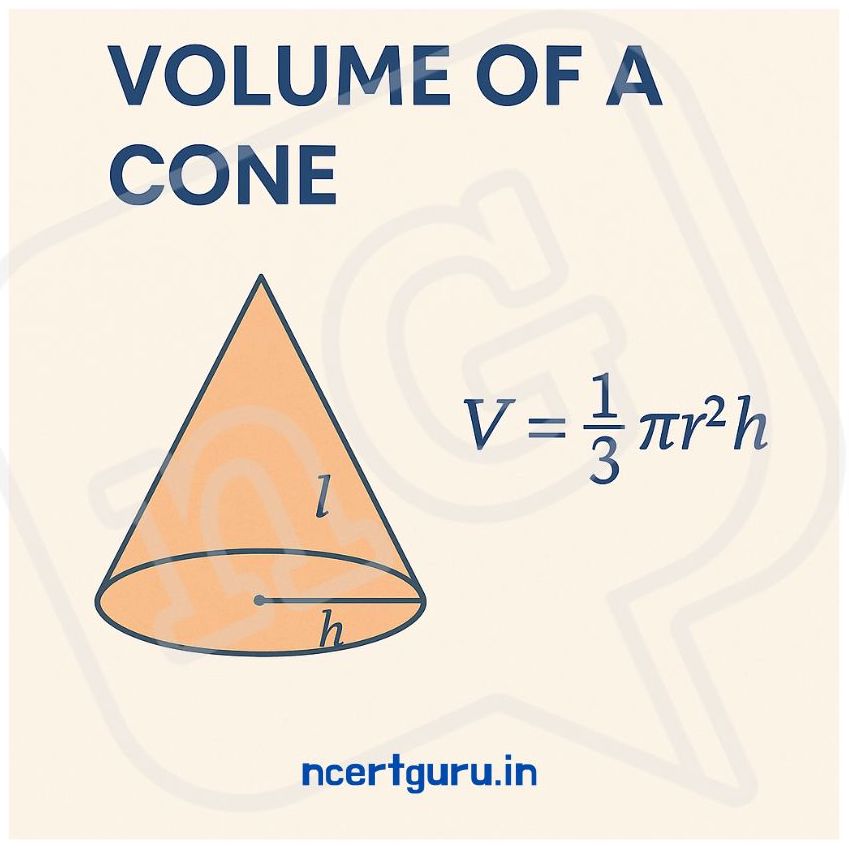
To find how much space is inside the cone, we use this formula:Volume of a Cone=13πr2hVolume of a Cone=31πr2h
Where:
- rr = radius of the base
- hh = height (from the base to the top)
- π≈3.14π≈3.14 or 227722
It means:
Take the area of the base (which is a circle), multiply by the height, then divide by 3.
📏 Why Divide by 3?
Because it takes three cones of the same size to fill one cylinder. So a cone holds one-third the space of a cylinder with the same base and height.
📌 Surface Area of a Cone
Let’s now learn how to find the amount of material needed to cover the outside of a cone.
There are two parts:
🔹 1. Curved Surface Area (CSA)
This is the outside curved part of the cone — like the paper wrapped around a party cap.
The formula is:Curved Surface Area=πrlCurved Surface Area=πrl
Where:
- rr = radius
- ll = slant height (side length from tip to base)
📌 Think of it like this: if you cut the cone and lay the curved part flat, it becomes a piece of a circle.
🔹 2. Total Surface Area (TSA)
This includes both:
- The curved surface, and
- The base (flat circular part)
So the formula is:Total Surface Area=πrl+πr2=πr(l+r)Total Surface Area=πrl+πr2=πr(l+r)
Super simple:
Just add the curved part and the base area!
Recap of Formulas for a Right Circular Cone
✔️ Volume of a Cone: 31πr2h
✔️ Curved Surface Area: πrlπrl
✔️ Total Surface Area: πr(l+r)πr(l+r)
👉 A right circular cone just means the cone’s top is right above the center of the base — it’s the cone shape we see in real life most often.
🧮 Volume of a Cone Example
Q: A cone has radius 3 cm and height 4 cm. Find its volume.
V=13πr2h=13×3.14×32×4=37.68 cm3
✏️Exercise 11.1 Solutions – Class 9 CBSE Maths
Chapter 11: Surface Areas and Volumes
These solutions focus on calculating the curved surface area (CSA) and total surface area (TSA) of right circular cones.
Formula Reference:
- Curved Surface Area (CSA) = πrl
- Total Surface Area (TSA) = πrl + πr² = πr(l + r)
- Slant height (l) = √(h² + r²)
- where r = radius, h = height, l = slant height
🔹1.Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
Given: Diameter = 10.5 cm, Slant height = 10 cm
Solution:
- Radius r = 10.5/2 = 5.25 cm
- CSA = πrl = (22/7) × 5.25 × 10 = 165 cm²
🔹2.Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is24m.
Given: Slant height = 21 m, Diameter = 24 m
Solution:
- Radius r = 24/2 = 12 m
- CSA = πrl = (22/7) × 12 × 21 = 792 m²
- TSA = CSA + Base area = 792 + πr² = 792 + (22/7) × 144 = 792 + 452.57 = 1244.57 m²
🔹3.Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find (i) radius of the base and (ii) total surface area of the cone.
Given: CSA = 308 cm², Slant height = 14 cm
Solution: (i) Find radius:
- r = CSA/(πl) = 308/((22/7) × 14) = 7 cm
(ii) Find total surface area:
- TSA = πr(l + r) = (22/7) × 7 × (14 + 7) = (22/7) × 7 × 21 = 462 cm²
🔹4.A conical tent is 10 m high and the radius of its base is 24 m. Find
(i) slant height of the tent.
(ii) cost of the canvas required to make the tent, if the cost of 1 m2 canvas is ` 70.
Given: Height = 10 m, Radius = 24 m
Solution: (i) Find slant height:
- l = √(r² + h²) = √(24² + 10²) = √(576 + 100) = √676 = 26 m
(ii) Find CSA and cost:
- CSA = πrl = (22/7) × 24 × 26 = 1977.14 m²
- Cost at ₹70 per m² = 1977.14 × 70 = ₹138,399.80
🔹5.What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm (Use π = 3.14).
Given: Height = 8 m, Radius = 6 m, Canvas width = 3 m
Solution: (i) Find slant height:
- l = √(r² + h²) = √(6² + 8²) = √(36 + 64) = √100 = 10 m
(ii) Find required canvas length:
- CSA = πrl = (22/7) × 6 × 10 = 188.57 m²
- Required length of canvas = 188.57/3 ≈ 62.86 m
- Adding 0.2 m for margins: Final length = 62.86 + 0.2 = 63.06 m
🔹6.The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of ` 210 per 100 m2.
Given: Slant height = 25 m, Diameter = 14 m
Solution:
- Radius r = 14/2 = 7 m
- CSA = πrl = (22/7) × 7 × 25 = 550 m²
- Cost at ₹210 per 100 m² = (550/100) × 210 = ₹1,155
🔹7.A joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
Given: Radius = 7 cm, Height = 24 cm, Number of caps = 10
Solution:
- Slant height l = √(r² + h²) = √(7² + 24²) = √(49 + 576) = √625 = 25 cm
- Area for 1 cap = πrl = (22/7) × 7 × 25 = 550 cm²
- Area for 10 caps = 550 × 10 = 5,500 cm²
🔹8. A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is ` 12 per m2, what will be the cost of painting all these cones? (Use π = 3.14 and take1.04 =1.02)
Given: 50 cones, Diameter = 40 cm, Height = 1 m (= 100 cm)
Solution:
Cost at ₹12 per m² = 9.17 × 12 = ₹110.04
Radius r = 40/2 = 20 cm
Height h = 100 cm
Slant height l = √(h² + r²) = √(100² + 20²) = √(10,000 + 400) = √10,400 ≈ 102 cm
CSA of one cone = πrl = (22/7) × 20 × 102 ≈ 1,834.29 cm² = 0.183429 m²
Total area for 50 cones = 50 × 0.183429 = 9.17 m²
